在最新的数学界轰动新闻中,一群来自清华的校友们借助 AI 的力量,成功证明了162个之前无人能解的数学定理。更厉害的是,这个名叫 LeanAgent 的智能体,竟然还攻克了陶哲轩对多项式 Freiman-Ruzsa 猜想的形式化难题!这让我们不得不感叹,基础科学的研究方法可谓是被 AI 彻底改头换面了。
众所周知,当前的语言模型(LLM)虽然炫酷,但大多依然是静态的,无法在线学习新知识,证明高等数学定理更是难如登天。然而,加州理工、斯坦福大学和华盛顿大学的研究团队联合开发的 LeanAgent,正是一个具备终身学习能力的 AI 助手,能够不断地学习和证明定理。
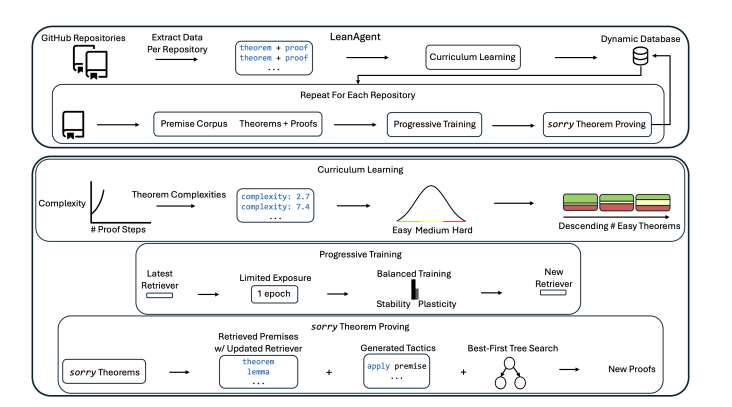
LeanAgent 通过精心设计的学习路径来应对不同数学难度,利用动态数据库管理源源不断的数学知识,确保它在学习新知识时不会忘记已经掌握的技能。实验表明,它成功从23个不同的 Lean 代码库中,证明了162个此前无人能解的数学定理,性能比传统的大模型高出了整整11倍,真是令人惊叹!
这些定理涵盖了高等数学的诸多领域,包括抽象代数和代数拓扑等棘手的问题。LeanAgent 不仅能够从简单概念入手,逐渐攻克复杂主题,还在稳定性和反向迁移方面展现了卓越的表现。
不过,陶哲轩的挑战依然让 AI 感到无奈。尽管交互式定理证明器(ITPs)如 Lean,在形式化和验证数学证明方面发挥着重要作用,但构建这样的证明过程往往复杂且耗时,需细致入微的步骤和大量数学代码库。像 o1和 Claude 这样的先进大模型面对非形式化证明时,也容易出现错误,这突显了 LLM 在数学证明准确性和可靠性上的短板。
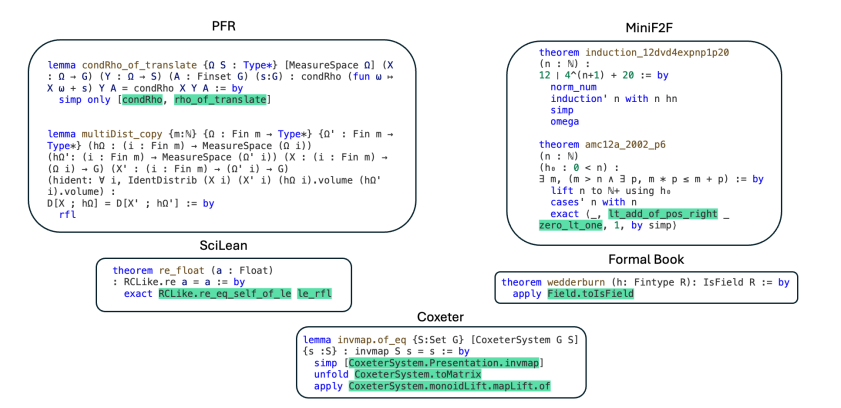
过去的研究尝试了使用 LLM 生成完整证明步骤,例如 LeanDojo,就是通过训练大模型在特定数据集上创建的定理证明器。然而,形式化定理证明的数据极为稀缺,限制了这种方法的广泛适用。另一项目 ReProver 则是针对 Lean 定理证明代码库 mathlib4优化的模型,虽然它涵盖了超过10万个形式化数学定理和定义,但仅限于本科数学的范围,因此在面对更复杂问题时表现不佳。
值得注意的是,数学研究的动态性给 AI 带来了更大挑战。数学家们通常同时或交替处理多个项目,比如陶哲轩就同时推进多个研究领域,包括 PFR 猜想和实数对称平均等。这些例子显示了当前 AI 定理证明方法的一个关键不足:缺乏一个能够在不同数学领域自适应学习和提升的 AI 系统,尤其是在 Lean 数据有限的情况下。
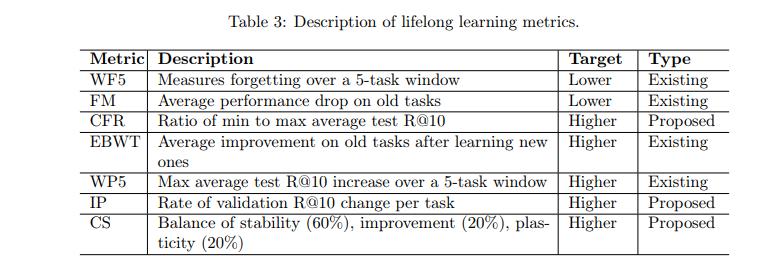
正因如此,LeanDojo 的团队创造了 LeanAgent,这是一个全新的终身学习框架,旨在解决上述难题。LeanAgent 的工作流程包括推导定理复杂度,以制定学习课程,通过渐进训练在学习过程中平衡稳定性与灵活性,并利用最佳优先树搜索来寻找尚未被证明的定理。
LeanAgent 与任何大模型结合使用,通过 “检索” 来提升其泛化能力。它的创新之处在于使用自定义动态数据库来管理不断扩展的数学知识,以及基于 Lean 证明结构的课程学习策略,助力学习更复杂的数学内容。
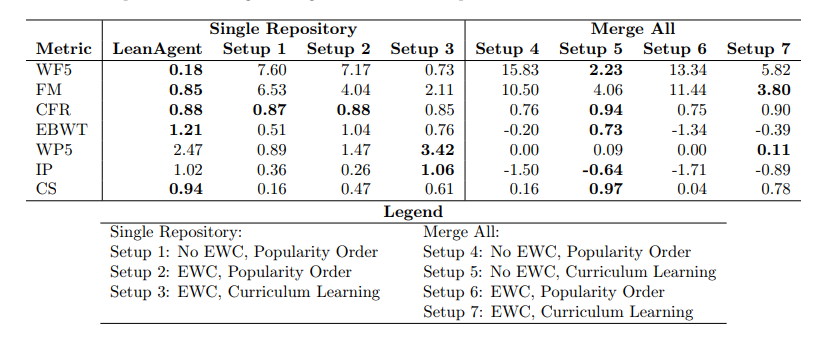
在应对 AI 的灾难性遗忘问题上,研究者采用了一种渐进训练的方法,使 LeanAgent 能够持续适应新的数学知识,同时不忘记先前的学习。这一过程涉及在每个新的数据集上进行增量训练,确保稳定性与灵活性达到最佳平衡。
通过这种渐进训练,LeanAgent 在证明定理方面的表现卓越,成功证明了162个尚未被人类解答的难题,尤其在抽象代数和代数拓扑的挑战性定理上大展身手。其在证明新定理的能力上比静态的 ReProver 高出11倍,且保持了对已知定理的证明能力。
LeanAgent 在定理证明的过程中表现出了渐进学习的特征,从简单的定理逐渐过渡到更复杂的定理,证明了它在数学知识掌握上的深度。例如,它证明了与群论和环论相关的基础代数结构定理,展现出对数学的深刻理解。总的来看,LeanAgent 以其强大的持续学习和改进能力,为数学界带来了令人兴奋的前景!
论文地址:https://arxiv.org/pdf/2410.06209